What Is Negative 1.5 as a Fraction
Decimal to Fraction Calculator
Convert a decimal to a fraction using our calculator by entering a decimal value below. The calculator shows all the work in the solution so you can see each step.
Fraction Result:
Steps to Convert Decimal to Fraction
Convert the decimal into a fraction by putting the decimal over 1 in fraction format
0.75 = .75 1
Multiply the numerator and denominator by 10 to eliminate decimal places
0.75 × 10 1 × 10 = 7.5 10
Multiply the numerator and denominator by 10 to eliminate decimal places
7.5 × 10 10 × 10 = 75 100
Reduce the fraction by finding the greatest common factor. The greatest common factor of 75 and 100 is 25
Divide the numerator and denominator by the greatest common factor (25)
75 ÷ 25 100 ÷ 25 = 3 4
Do you want to convert fraction to decimal?
How to Convert a Decimal to a Fraction
Decimal and fractional numbers both represent a number that is not an even integer or a number that is not a whole number. Every decimal number can be converted to a fraction in just three easy steps.
Note that the process of converting a repeating decimal is different.
Step One: Create the Starting Fraction
The first step in transforming a decimal to a fraction is creating a starting fraction with the decimal as the top number and 1 as the bottom number.
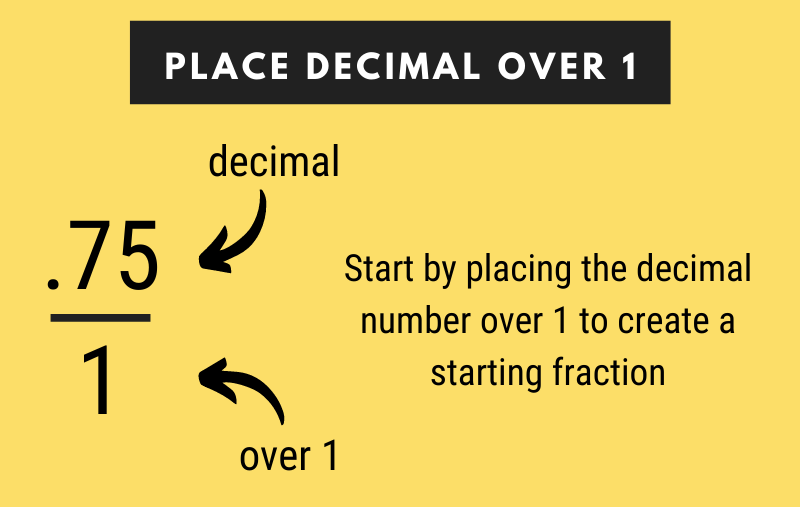
For example, to convert .75 to a fraction, start by making a fraction with .75 as the numerator and 1 as the denominator.
.75 = .75 1
Step Two: Multiply by Ten
The next step is to multiply the numerator and the denominator by 10 to eliminate the decimal place. Continue multiplying both by 10 until the numerator is a whole number.

Continuing the example from above, let's convert .75 1 to 75 100
.75 1 = (.75 × 10) (1 × 10) = 7.5 10
7.5 10 = (7.5 × 10) (10 × 10) = 75 100
Step Three: Reduce the Fraction
The final step in converting a decimal to a fraction is to reduce or simplify the fraction. To reduce, find the greatest common factor for the numerator and denominator. Then, divide both the numerator and the denominator by the greatest common factor.

To complete the example above, we know that the greatest common factor of 75 and 100 is 25. So, let's divide the numerator and denominator by 25 to solve the reduced fraction.
75 100 = (75 ÷ 25) (100 ÷ 25)
75 100 = 3 4
Here's a tip: use our fraction simplifier to easily reduce your fraction.
For negative numbers, remove the negative symbol from the starting decimal, then follow the steps above. After converting to fraction form, add the negative sign back.
How to Convert a Repeating Decimal to a Fraction
Repeating decimal numbers require a slightly different process to convert to a fraction. A repeating decimal is a decimal number that continues infinitely, such as 1.1787878.
These numbers are usually expressed in a rounded form, such as .788, or with an over-bar like this: 1.178.
Step One: Create an Equation
The first step in transforming a repeating decimal is to create an algebraic equation to represent the decimal.
For example, let's convert the decimal 1.178 into a fraction. Start by creating an equation to assign the expression 1.1787878 to x.
x = 1.1787878
Step Two: Multiply by 10 Until the Repeating Decimal is on the Left
The second step is to continue multiplying both sides of the equation by 10 until the repeating number is on the left side of the decimal point.
If there are multiple repeating numbers that repeat in a pattern, then multiply by 10 until the repeating pattern is on the left side of the decimal point.
Continuing the example above, let's multiply both sides of the equation by 10 until the repeating "78" part of the decimal is on the left side of the decimal point.
x = 1.1787878
10 × x = 10 × 1.1787878
10x = 11.787878
10 × 10x = 10 × 11.787878
100x = 117.87878
10 × 100x = 10 × 117.87878
1000x = 1178.78
Step Three: Multiply by 10 Until the Repeating Decimal is on the Right
The third step is to create a new equation for x and multiply until the repeating decimal portion is to the right of the decimal point
Building on our example, multiply both sides of the equation by 10 until the repeating "78" part of the decimal is on the right side of the decimal point.
x = 1.1787878
10 × x = 10 × 1.1787878
10x = 11.78
Step Four: Combine the Equations
The next step is to combine the equations and move both x variables to the left and both decimal values to the right.
Let's combine the equations and solve.
1000x – 10x = 1178.78 – 11.788
Step Five: Solve
Finally, solve for x to convert the decimal value to a fraction.
Let's combine the equations and solve.
1000x – 10x = 1178.78 – 11.78
990x = 1167
990x 990 = 1167 990
x = 1167 990
Decimal to Fraction Conversion Table
An alternate method to convert a decimal to a fraction is to use a conversion table such as this one. See the fraction equivalents for some common decimal values below. The table allows you to conveniently see the corresponding fraction for a decimal number.
| Decimal Value | Fraction Value |
|---|---|
| 0.0625 | 1/16 |
| 0.08333 | 1/12 |
| 0.1 | 1/10 |
| 0.111 | 1/9 |
| 0.125 | 1/8 |
| 0.1666 | 1/6 |
| 0.2 | 1/5 |
| 0.222 | 2/9 |
| 0.25 | 1/4 |
| 0.333 | 1/3 |
| 0.375 | 3/8 |
| 0.4 | 2/5 |
| 0.444 | 4/9 |
| 0.5 | 1/2 |
| 0.555 | 5/9 |
| 0.6 | 3/5 |
| 0.625 | 5/8 |
| 0.666 | 2/3 |
| 0.75 | 3/4 |
| 0.777 | 7/9 |
| 0.8 | 4/5 |
| 0.8333 | 5/6 |
| 0.875 | 7/8 |
| 0.888 | 8/9 |
See more fraction decimal equivalents.

What Is Negative 1.5 as a Fraction
Source: https://www.inchcalculator.com/decimal-to-fraction-calculator/